(Python)-初學 Class-8 — 遞迴

(Python)-初學 Class-8 — 遞迴
在解決問題時,我們經常會遇到無法輕鬆使用 loop 或是 if statement就能處理的問題,像是走迷宮問題遇到死路時需要回到上一層計算、或是在解決河內塔問題時儘管操作相同,卻因為每次要進行操作的參數不同而需要寫重複的程式碼等等。此時,一個經常被納入考慮的方法,就是利用遞迴的概念來撰寫一個函式。
如果你對於函式還不甚了解,歡迎參考 Python 初學 Class-7—函式來輔助在遞迴函式上的學習。
8-1 遞迴的基本概念
有時我們解決一個問題的方法是將其拆解,再各自將小問題解決以後得到答案,這樣的概念我們稱之為 “Divide and Conquer”,中文稱為分治法。
遞迴這個方法就是依據此概念形成的:我們將一個龐大的問題切分成數個相似的中問題,然後將中問題再區分成許多小問題,再將這些小問題用同一個 function 解決,最終將這個大問題處理完,這個處理方式就稱作 recursion。
在數學以及電腦科學的領域當中,當一個函式會在執行當中,會不斷地自己呼叫自己時,我們便認為這個函式具有遞迴的性質。同時,為了避免函式永無止盡地自我呼叫 (self-calling),我們也需要設計一個明確的終止條件。因此,我們便得到了設計一個遞迴函式的兩個重點:遞迴自我呼叫的方式以及結束呼叫的終止條件。
8-2 實作 recursion 函式
以下我們將討論三個經典的遞迴問題,階乘、費氏數列以及最大公因數。
1. 階乘 Factorial
階乘問題是我們從高中就學過的數學問題, n 階 n!代表的即是從 1 開始連乘直到 n 為止,意即 n! = 1 x 2 x … x n 。
當我們需要用程式來幫助我們寫出一個計算階乘的函式,大家可能會先想到的是迴圈,在這個函式當中,我們只需要一個 n 次的 for loop 就可以解決這個問題。在函式當中設定一個變數用來記住目前的乘積,然後從 1 開始乘直到 n 為止,程式碼可能如下:
Learn 1 :
def factorial_loop (n):
factor = 1
for i in range(1,n+1):
factor *= i
return factor
print(factorial_loop(3))
6
於此同時,我們也可以利用 recursion 來解決這個問題。
我們再重新檢視 n 階乘這個算式:
n! = 1 x 2 x … x (n-1) x n
如果我們將乘上 n 以前的乘積拿出來看:
n! = [1 x 2 x … x (n-1)] x n = (n-1)! x n
不正是 n-1 階乘上 n 嗎!也就是說,我們想要得到 n 階,只要得到 n-1 階的乘積以後再乘上 n 即可。
以此類推, n-1 階來自於 n-2 階乘上 n-1、…、 2 階等於 1 階乘上 2。那麼 1 階呢? 0 階呢?這兩者從我們高中所學的數學可以得知,我們將兩者皆定義為 1 。

到這裡是否有點眉目了呢?當我們想要求得 n 階乘,只需要找到 n-1 階的階乘,但此時我們就需要找到 n-1 階的答案,便需要轉而尋求 n-2階…直到我們所要尋找的是 1 階為止。如果我們使用數學式來將我們的問題釐清,可能會是如下的式子:
0! = 1 1! = 1 n! = n * (n-1)!, n >= 1
那我們該如何將剛才所說的事情寫成一個遞迴的程式碼呢?首先,我們要先思考,在甚麼條件底下我們不會繼續呼叫自己算出 n-1 階的答案呢?答案是 n = 1 以及 n = 0 的時候,我們已經將之定義為 1 了。其他時候我們都需要呼叫自己算出 n-1 階的階乘用以乘上現在的 n ,而程式碼我們試寫如下:
Learn 2 :
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial(n - 1)
print(factorial(4))
24
這個程式碼的閱讀上是不是比迴圈版本的容易理解了呢?
factorial(n)這個函式的定義如下:參數 n 是 1 或 0 的話,就回傳 1 ;不是的話就 return n 乘上用 n-1 當作參數呼叫自己的回傳值,也就是 factorial(n-1) 。看起來是不是和我們方才所列的數學式十分相似呢?
接著讓我們再來寫出下一個遞迴函式吧!
2. 費氏數列 Fibonacci sequence
費氏數列也是在傳達遞迴概念時,經常被提及的一個問題。所謂的費波那契數列,指的是一個數列,每一項都等於他的前兩項的和,也就是說第 n 項等於第 n-1 項以及第 n-2 項的和。
費氏數列的數學式如下:
f(0) = 0, f(1) = 1 f(n) = f(n-1) + f(n-2), n>=2
而我們的問題就是給定整數 n ,希望得到費氏數列第 n 項的值。這一次我們不妨直接來構思該如何寫出這一個遞迴函式吧!
首先,我們想要求得的是第 n 項的值,也就是我們的函式參數為整數 n ,它每一次都會呼叫以 n-1 為參數以及 n-2為參數的函式,並且將他們的回傳值相加起來再 return 。但若參數值為 1 或是 0 ,根據費氏數列的定義,我們就要直接回傳 1 和 0 。聽起來十分簡單,試寫程式碼如下:
Learn 3 :
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
n = int(input())
print(fibonacci(n))
7 13
基本上與我們對於費氏數列數學式的理解相差無幾,執行結果如上:
解釋完了遞迴的想法,不妨來思考要如何利用迴圈來解決同樣的問題吧!我們的程式碼可能長這個樣子:
Learn 4 :
def fibonacci_loop(n):
if n == 1 or n == 2:
return 1
else:
fib1 = 1
fib2 = 1
fib3 = 0
for i in range(2, n):
fib3 = fib1 + fib2
fib1 = fib2
fib2 = fib3
return fib3
n = int(input())
print(fibonacci_loop(n))
7 13
對於要將前兩項加起的定義,我們使用兩個變數 fib1 以及 fib2 來記住,然後將 fib3 存取加起來的和,然後不斷往後推直到 fib1 和 fib2 分別等於第 n-2 項以及第 n-1 項。如果這樣字面上解釋有些難以理解,不妨在自己嘗試的過程當中印出每一次的 fib1 、fib2 、fib3 ,相信更能理解這一個函式的思維。
使用迴圈所寫的程式碼想法依舊不難,只是相較於遞迴的寫法而言,程式碼閱讀起來稍微不那麼直觀一些。
最後我們再來看一個同樣經典的例子,最大公因數。
3. 最大公因數 GCD
相信大家對於最大公因數的概念並不陌生,就是給定兩個整數,要求找到兩者共同的最大因數。
尋找的方法很多,有些人會從較小者每次減一然後進行檢查、有些人利用質因數分解來尋找答案,另一些人可能會使用一個特殊的方法——輾轉相除法。如果你對於輾轉相除法的用法不甚了解,建議你可以去維基百科或是努力推廣數學知識的昌爸工作坊來了解一下他的使用方式。
將其方法解釋得簡單一點即是,每一次都用兩者間較小的數去對另一個數取餘數,然後再用這個餘數以及剛才我們所選的較小的數進行和方才相同的步驟。
不知道你有沒有注意到,輾轉相除法其實就是一個遞迴的方法,我們不斷的利用較小的數以及餘數來 “呼叫” 下一層,直到取得的餘數為零為止,代表我們找到了所要的答案。基於此想法,我們試寫的函式如下:
Learn 5 :
def gcd(m, n):
if n == 0:
return m
else:
return gcd(n, m%n)
num1 = int(input())
num2 = int(input())
print(gcd(num1, num2))
10 45 5
在能被整除以前,我們都會不斷地以目前被用於取餘數的數字以及取得的餘數來呼叫自己,終止條件即是整除,也就是取餘數等於零。
遞迴的限制與複雜度問題
在瞭解了遞迴的概念以及使用方式以後,讓我們來談一談遞迴函式的複雜度問題,以及隨之而來對於 recursion 的限制。
4.recursion 的複雜度問題
在了解了遞迴函式的概念以後,不知道大家是否也都有感受到遞迴有著理解上簡單明瞭,又可以縮短程式碼長度的好處。
那麼,為什麼在多數遞迴可以處理的問題當中,大家還是比較常使用迴圈而不是遞迴呢?
再讓我們溫習一下剛才費氏數列的例子:
#遞迴解
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
我們可以看到,在程式碼當中,這一個函式呼叫了兩次自己。但是與此同時,在進行下一層的計算以前,我們還要先記得等等下一層的函式回傳回來以後,我要將兩個回傳值相加。也就是說,在參數為 n 時,我們呼叫了 fibonacci(n-1) 以及 fibonacci(n-2) ,並且在真的計算 fibonacci(n-1) 以及 fibonacci(n-2) 之前,還要先記住這裡要將他們加起來。
很顯然地,在這一個遞迴函式裡,我們在知道要計算 fibonacci(n-1) + fibonacci(n-2) 時,要等到將 fibonacci(n-1) 以及 fibonacci(n-2) 都計算完以後,再回來這裡將兩個回傳值相加起來。但是電腦要怎麼知道等到得到回傳值以後,我們要將它相加呢?那就是因為電腦在看到 fibonacci(n-1) + fibonacci(n-2) 時就已經記住了等等要相加,才開始計算 fibonacci(n-1) 以及 fibonacci(n-2) 。而這個 “記住” 的動作當然會花電腦的記憶體,等到函式得到回傳值以後再從記憶體當中拿出來。也就是說,電腦在一層一層從參數為 n 、n-1、…一直計算到 fibonacci(1) 以前,需要記住 n 這麼多個加,除此之外,在其他的遞迴問題當中可能還會需要記住其他數字等等,總之需要將每一層的數值、操作等等都存在電腦暫時的記憶體當中。
除了遞迴本身需要記住每一層的資訊以外,有時我們還可能讓電腦做重複的事情。同樣使用剛才費氏數列的例子,我們在計算第 n 項的值時需要計算第 n-1 項以及第 n-2 項的數值,而第 n-1 項的值又來自於 n-2 以及 n-3 項,第 n-2 項的計算又要用到第 n-3 項以及第 n-4 項…
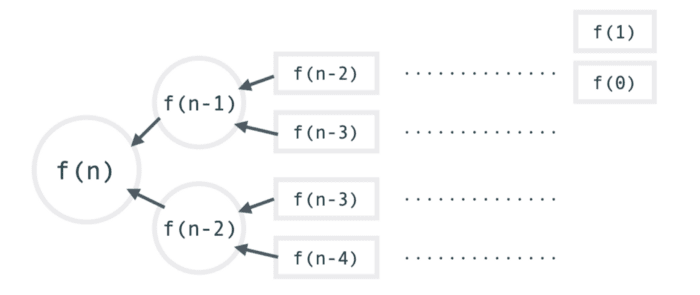
然而,電腦並沒有聰明到記得你剛才想要計算 f(n)的時候已經呼叫過 f(n-2) 了,在你呼叫 f(n-1) 時又會呼叫 f(n-2) 一次,因此光是 f(n-2) 這個函式就執行了兩次。而 f(n-3) 更是在計算 f(n-1) 時被呼叫一次,然後在計算兩次 f(n-2) 時又被各自呼叫一次…更別提最後的f(1) 、 f(0) 會被呼叫多少次了!
而且這些函式所回傳的值也通通都會被存在記憶體裡直到同一層的函式都被執行完為止,因此佔用了大量的空間,而且經常會把曾經做過的事情又拿來重新做一遍,不只浪費時間,也浪費空間,造成了程式的不效率(inefficiency)。
接著讓我們比較一下迴圈的寫法吧!
#迴圈解
def fibonacci_loop(n):
if n == 1 or n == 2:
return 1
else:
fib1 = 1
fib2 = 1
fib3 = 0
for i in range(2, n):
fib3 = fib1 + fib2
fib1 = fib2
fib2 = fib3
return fib3
在這一個迴圈的解法當中,只額外使用了三個整數的儲存空間,並且免去了呼叫其他函式的時間,也不用暫且記住這一個函式的數值以等待其他函式計算完成,更不用做完全相同的事情,這個 loop 完成的同時,這個函式也就基本上結束了。
用比較電腦科學的話來講,就是遞迴這樣的方法會增加時間複雜度 (time complexity) :在這個費氏數列的例子底下,使用迴圈解時,隨著我們輸入的 n 變大 m 倍,也只是迴圈多跑 m 倍的次數而已,也就是說時間的增加是線性的 (linear-time);但是在遞迴解的情況底下, m 倍的 n 所增加的時間可不只是 m 倍而已,而是指數增加 (exponential-time)。於此同時,遞迴的使用也會增加空間複雜度 (space complexity)。
5. recursion 的使用限制
最後,讓我們來談談 recursion 使用的限制吧!如同我們前面所說的, recursion 的概念即是不斷地呼叫自已,電腦必須要利用記憶體先替你記住這一層的中間值,然後去下一層繼續進行計算,直到終止條件被滿足。然而,萬一我們不小心參數過大、 recursion 設計不良使得終止條件一直沒有被滿足或是像方才所提的記住了太多重複的東西的話,電腦裡的計算資源不就通通都被 recursion 所佔滿了嗎?
為了避免這件事情的發生, Python 對於遞迴次數(或者可以稱之為深度)有所限制,也就是說,它透過限制呼叫遞迴函式的次數,來達成杜絕你的遞迴無止盡地跑下去這個可能性。透過 sys 這個 module 當中的函式,我們可以了解到 Python 對於遞迴的限制次數是 3000 次。
Learn 6 :
import sys
print(sys.getrecursionlimit())
3000
假如你超過了這個次數的限制,可能會遇到 RecursionError: maximum recursion depth exceeded 這樣的 error。目前為止大家所撰寫的程式應該都還不需要、也不建議大家使用需要遞迴次數太多的函式,因此,如何增加其次數上限的方法我們在這裡就姑且不談。
小結
最後,讓我們來總結一下遞迴這個讓人又愛又害怕的概念吧!
基本上,大多數能被遞迴解決的問題,都可以找出迴圈解。如果使用遞迴的概念解題,通常可以將艱難的問題用簡單的想法解決;但是使用迴圈來改寫的話,通常可以增進程式運行的效率。有一句話是這麼說的:
To iterate is human,to recurse divine. — — L. Peter Deutsch
iterate 的意思是迭代,或著目前來說我們可以用迴圈的想法來理解這個概念。這句話想要表達的究竟是什麼呢?是指迴圈解較容易想出來,遞迴解需要靈光一現、相對需要思考嗎?還是想表達迴圈解在閱讀上顯得有些冗長不平易近人,遞迴解優美又簡潔?抑或是想比較兩者之間的什麼特質呢?
總歸一句話,當我們在解決問題的同時,遞迴與迴圈的選擇值得我們深思。
免責聲明:
1.本影像檔案皆從網上搜集轉載,不承擔任何技術及版權問題
2.如有下載連結僅供寬頻測試研究用途,請下載後在24小時內刪除,請勿用於商業
3.若侵犯了您的合法權益,請來信通知我們,我們會及時刪除,給您帶來的不便,深表歉意。